最高のコレクション 数学 円順列 338750

答え 円順列と確率 Piece Check 16 17 東大数学9割のkatsuyaが販売する高校数学の問題集
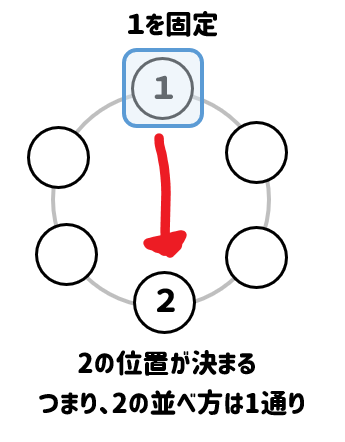
31/1/17 円の一か所を固定して考える 上では、円順列を考えるときに、一列に並べてから円形に並べなおす、という考え方をしました。 ここでは、少し違う考え方をしてみましょう。 円形に並べる場合には、クルクルと回転させて同じになるものを同一視し( m − n)!
数学 円順列
数学 円順列-高校数学Aで学習する場合の数の単元から 「平面、立体の塗り分け」 についての問題をまとめておきます。 今回の記事を通して、問題の解き方を身につけていきましょう。 取り上げる問題はこちら! 問題① 下の図のように4個の部分に区切った紙21/8/17 順列の特訓プリントです (`・ω・´) 図を描くのが解くためのカギです (*´ω`*) 数学A 順列 人を並べる特訓① 数学A 順列 桁数問題特訓① 数学A 順列 辞書式配列・小さい順特訓① 数学A 順列 円順列 (人を並べる)特訓① 数学A 順列 円順列 (図形の色塗り)特訓①

黄チャート 円順列 確率 Clearnote
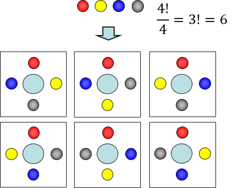
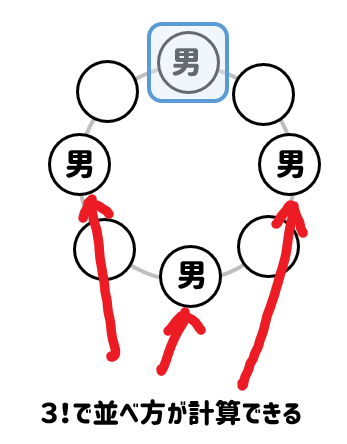
3/8/18 円順列とは? その名の通り、円の様に(主に人など)を並べる順列の事です。 順列があいまいな人は、「順列と組み合わせの違い」をチェック! 普通の順列と円順列の違い 今回一番大事なところです。普通、順列は 初めと終わりがあります 。5/5/19 なぜなら 配置は変わっています が 「順列」としての順番は崩れていない からです。 このように、「円」のまわりなどの特殊な状況では、異なるように見える順列も同じとしてカウントしなくてはいけません。 このような順列を 円順列 といいます。 ですから今の例でいうと はすべて同じなので1パターンと数えます。 となると明らかに 1 通りは数え順列を用いて求めることができます。 よって, (通り) このように,円順列では (全体の人数- 1) の階乗として並び方の総数を求めることができます。 (イ) 2 人が隣り合わない場合の求め方としては, ① 余事象の考え方を用いる
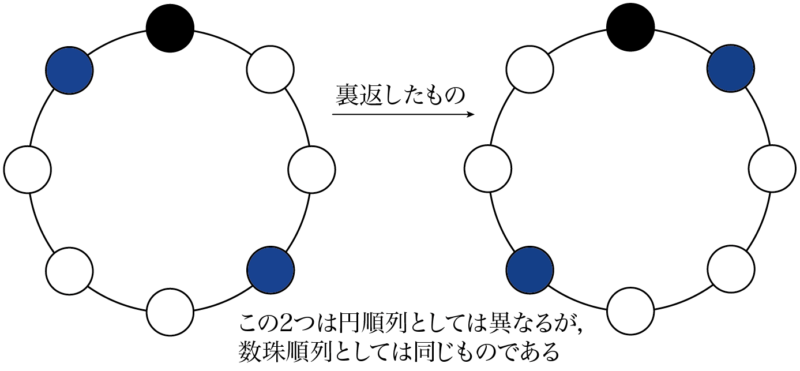
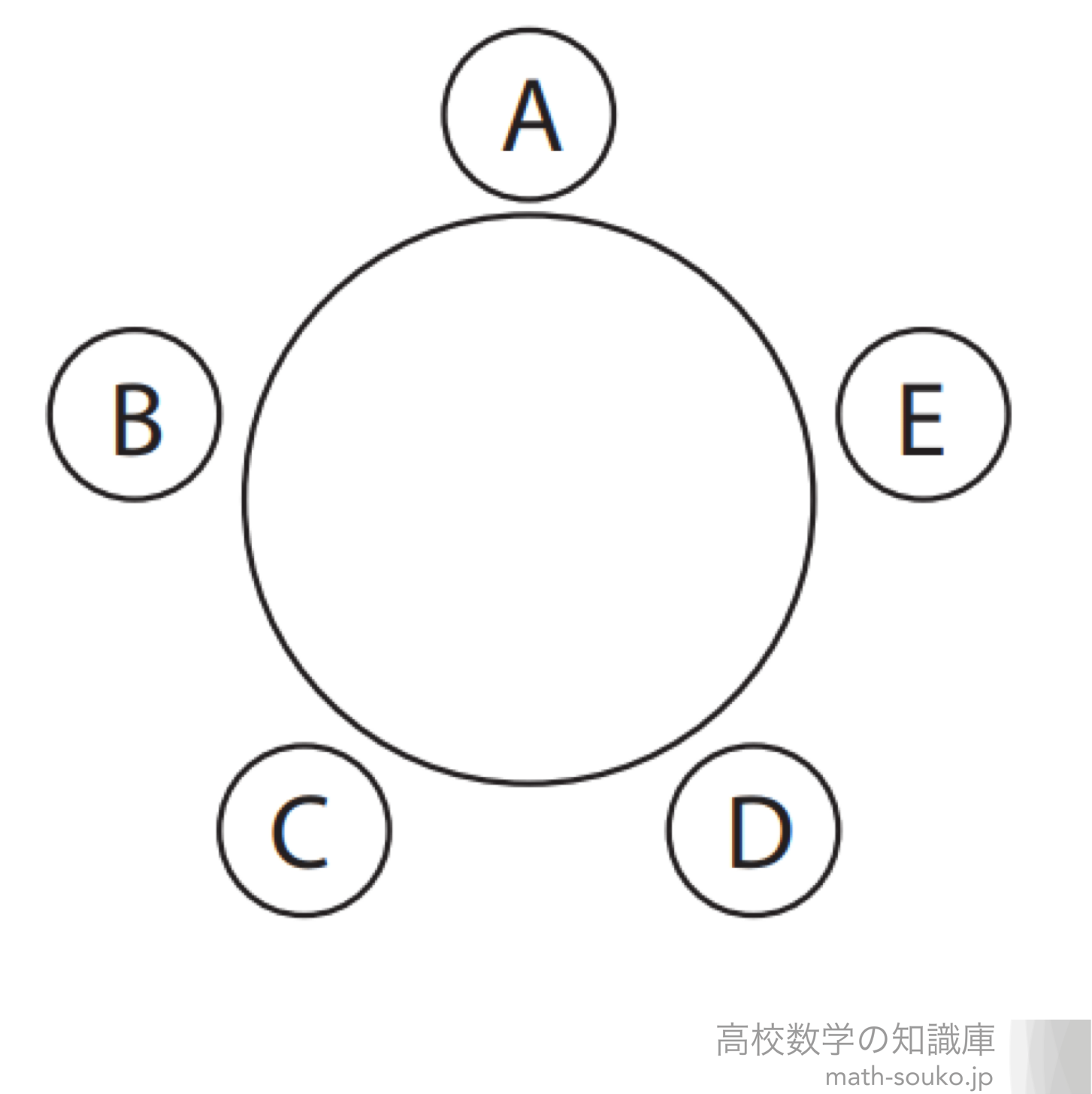
21/7/21 円順列 とは、 いくつかの異なるものを円形に並べる順列 のことです。 たとえば、複数の人が円形のテーブルに沿って座る場合が円順列です。 一般に、 円順列の総数 は以下のように定義されこの順列は\( n \)個の中から\( r \)を取り、一列に並べる場合の数の総数である。 では、取り出した\( r \)個を一列ではなく、円に並べた場合はどうなるのであろうか? このように、いくつかのものを円形に並べた配列を 円順列 または、じゅず順列と呼ぶ13/3/17 円卓に座るというのは、 標準円形に並べる(円順列) で見た「円順列」の問題です。 回転して同じ座り方になるものを除く 必要があります。 まずは、円卓の座り方が全部で何通りあるかを考えます。 数え方はいろいろありますが、 一人を固定して 考えてみましょう。 とりあえず、A に注目しましょう。 A を基準に、他の4人がどう座るかを考えます
数学 円順列のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary | 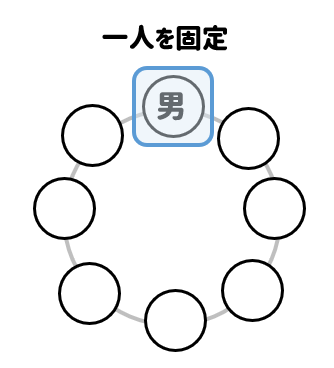 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 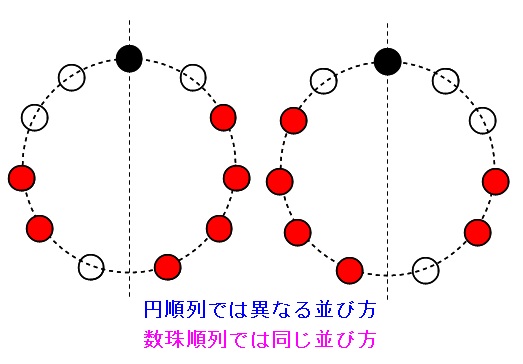 円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 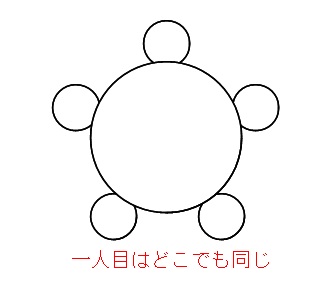 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 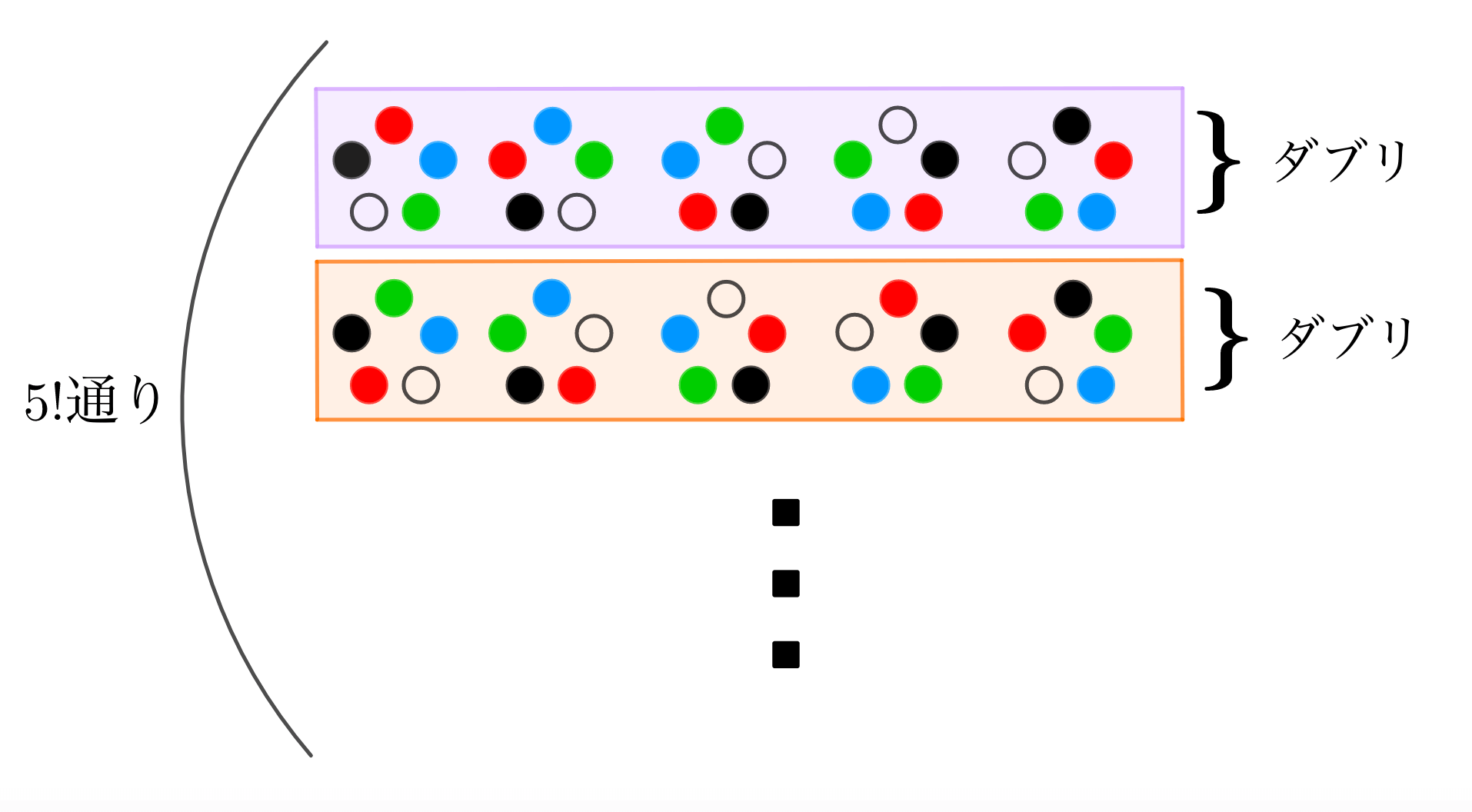 円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary | 円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
「数学 円順列」の画像ギャラリー、詳細は各画像をクリックしてください。
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
 円順列とじゅず順列 4 Schoolmath S Diary |  円順列とじゅず順列 4 Schoolmath S Diary |
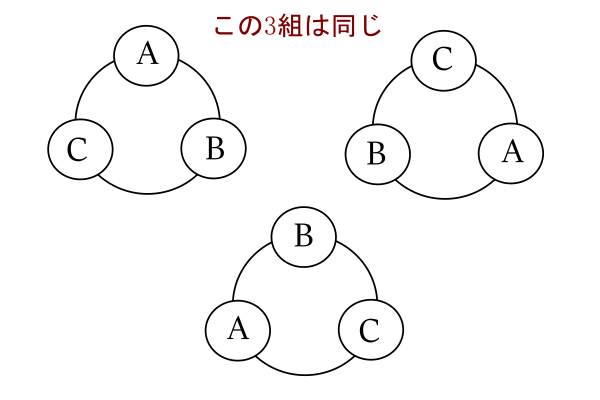
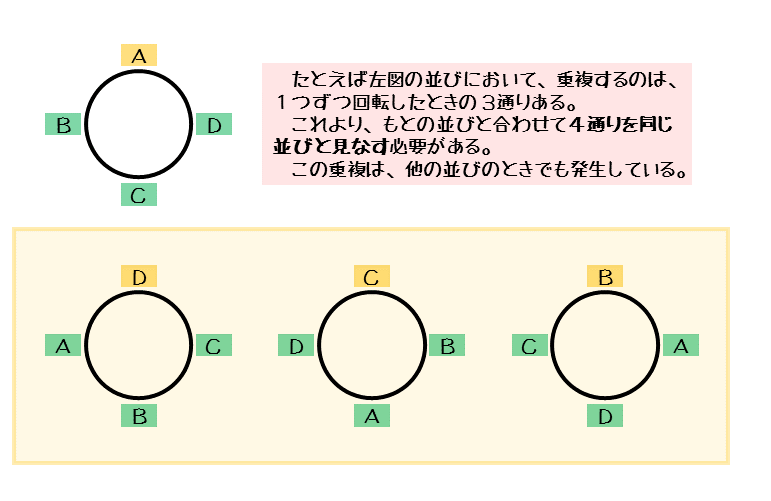
18/4/ このとき x, y, z の組合せは ( x, y, z) = ( 1, 1, 4), ( 1, 2, 3), ( 2, 2, 2) の3通りになる。 考えやすいものから1つずつ確認していく。 ( 2, 2, 2) は数字の入れ替えがそもそもないため,円順列としても1通りである。 ( 1, 1, 4) に対して入れ替えを考えると,他に ( 1, 4, 1), ( 4, 1, 1) が考えられるから,次の3つの図のようになる。 3つの並べ方は異なるように見えるが,回転難しい重複円順列の一般的解法 重複円順列の考え方 周期解決法とコーシー・フロベニウス定理 松本睦郎(札幌啓成高等学校 講師) Episode1 難しい重複円順列 大学への数学14 年10 月号「秋の夜長に数え歌」(P12~)に次のような重複円順列の問題があっ た。
コメント
コメントを投稿